En 2012, el matemático Ian Stewart salió con un libro excelente y profundamente investigado titulada " En busca de lo Desconocido: 17 ecuaciones que cambiaron el mundo ."
Su libro da un vistazo a las ecuaciones más fundamentales de todos los tiempos, y los pone en un ser humano, en lugar de contexto técnico.
"Las ecuaciones sin duda puede ser aburrido, y que puede parecer complicado, pero eso es porque a menudo se presentan en una forma aburrida y complicada", dijo Stewart a Business Insider. "Tengo una ventaja sobre los profesores de matemáticas de la escuela: No estoy tratando de mostrar cómo hacer las sumas a ti mismo."
Explicó que cualquiera puede "apreciar la belleza y la importancia de las ecuaciones sin saber cómo resolverlos ... La intención es ubicar en su contexto cultural y humano, y tire hacia atrás el velo sobre sus efectos ocultos en la historia."
Stewart continuó que "ecuaciones son una parte vital de nuestra cultura Las historias detrás de ellos -. Las personas que descubrieron o inventaron ellos y los períodos en los que vivían - son fascinantes."
Aquí hay 17 ecuaciones que cambiaron el mundo:
El teorema de Pitágoras

¿Qué significa? El cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de sus piernas.
Historia: Aunque atribuido a Pitágoras, no es cierto que él fue la primera persona que lo demuestran. La primera prueba clara de vino de Euclides, y es posible que el concepto se conoce 1.000 años antes de Pythoragas por los babilonios.
Importancia: La ecuación está en la base de gran parte de la geometría, lo vincula con el álgebra, y es el fundamento de la trigonometría. Sin ella, la topografía exacta, la cartografía y la navegación serían imposibles.
En términos de matemáticas puras, el Teorema de Pitágoras define, la geometría euclidiana del plano normal. Por ejemplo, un triángulo rectángulo dibujado en la superficie de una esfera como la Tierra no necesariamente satisface el teorema.
El uso moderno: La triangulación se utiliza para este día para determinar la ubicación relativa de navegación GPS.
El logaritmo y sus identidades

¿Qué significa? Puede multiplicar números mediante la adición de números relacionados.
Historia: El concepto inicial fue descubierto por el escocés Laird John Napier de Merchiston en un esfuerzo por hacer que la multiplicación de los grandes números, a continuación, increíblemente tedioso y lento, más fácil y más rápido.Más tarde se perfeccionó por Henry Briggs para hacer tablas de referencia más fácil de calcular y más útil.
Importancia: Los logaritmos fueron revolucionarios, por lo que el cálculo más rápido y preciso para los ingenieros y astrónomos. Eso es menos importante con el advenimiento de las computadoras, pero siguen siendo un elemento esencial para los científicos.
Modernos de uso: Los logaritmos y las funciones exponenciales relacionados, se utilizan para modelar todo de interés compuesto para el crecimiento biológico de la desintegración radiactiva.
Cálculo

¿Qué significa? Permite el cálculo de una tasa de cambio instantánea.
Historia: Cálculo como la conocemos actualmente fue descrito en la misma época en el siglo 17 por Isaac Newton y Gottfried Leibniz. Hubo un largo debate sobre el plagio y la prioridad, que nunca podrá ser resuelto. Utilizamos los saltos de la lógica y partes de la notación de los dos hombres de hoy.
Importancia: Según Stewart, "Más que cualquier otra técnica matemática, se ha creado el mundo moderno." El cálculo es esencial en nuestra comprensión de cómo medir sólidos, curvas y áreas. Es la base de muchas de las leyes naturales, y la fuente de las ecuaciones diferenciales.
El uso moderno: Cualquier problema matemático donde se requiere una solución óptima. Esencial para la medicina, la economía, la física, la ingeniería y la informática.
la ley universal de la gravitación de Newton

¿Qué significa? Calcula la fuerza de gravedad entre dos objetos.
Historia: Isaac Newton derivó sus leyes sobre la base de principios de trabajo astronómico y matemático Johannes Kepler. También utilizó, y, posiblemente, un plagio de la obra de Robert Hooke.
Importancia: Se utiliza técnicas de cálculo para describir cómo funciona el mundo. A pesar de que más tarde fue suplantada por la teoría de la relatividad de Einstein, todavía es esencial para una descripción práctica de cómo los objetos en el espacio, como estrellas, planetas y naves espaciales hecho por el hombre, interactúan entre sí. La usamos para el día de hoy para diseñar las órbitas de los satélites y sondas.
Filosóficamente, la ley de Newton es importante porque describe cómo la gravedad funciona en todas partes, desde una pelota que cae al suelo en la Tierra a la evolución de las galaxias y el universo en su conjunto. Mientras tomamos la idea de las leyes universales para concedido hoy, en épocas anteriores la idea de que los mundos terrestres y celestes comparte las mismas propiedades fue revolucionario.
El uso moderno: Aunque, como se ha mencionado anteriormente, para usos prácticos ley de Newton ha sido aumentada por las teorías de Einstein, la idea básica de la gravedad newtoniana sigue siendo una aproximación útil para saber cómo se comportan las cosas en el espacio.
Números complejos

¿Qué significa? Matemáticos pueden ampliar nuestra idea de qué son los números mediante la introducción de las raíces cuadradas de números negativos.
Historia: Los números imaginarios se postuló originalmente por el famoso jugador / matemático Girolamo Cardano, luego se expandió por Rafael Bombelli y John Wallis. Todavía existían como un problema peculiar, pero esencial en matemáticas hasta que William Hamilton describió esta definición.
Los números imaginarios y complejos son matemáticamente muy elegante.Álgebra funciona a la perfección la forma en que queremos que - cualquier ecuación tiene una solución número complejo, una situación que no es cierto para los números reales: x2 + 4 = 0 no tiene solución número real, pero tiene una solución compleja: la plaza raíz de -4, o 2i. Cálculo se puede extender a los números complejos, y al hacerlo, nos encontramos con algunas simetrías y propiedades de estos números increíbles.
Importancia: Según Stewart ".... más moderna tecnología, desde la luz eléctrica a las cámaras digitales no podría haber sido inventado sin ellos." La extensión del cálculo de los números complejos, una rama de las matemáticas llamada "análisis complejo," es esencial para la comprensión de los sistemas eléctricos y una variedad de modernos algoritmos de procesamiento de datos.
El uso moderno: Se utiliza ampliamente en la ingeniería eléctrica y la teoría matemática.
La fórmula de Euler para poliedros

¿Qué significa? Describe una relación numérica que es cierto de todas las formas sólidas de un tipo particular.
Historia: Este fue desarrollado por el gran matemático Leonhard Euler siglo 18.Poliedros son las versiones tridimensionales de los polígonos, como el cubo a la derecha. Los vértices de un poliedro se llaman sus vértices, las líneas que conectan los vértices son sus bordes, y los polígonos que están cubriendo sus rostros.
Un cubo tiene 8 vértices, 12 aristas y 6 caras. Si añado los vértices y las caras juntas, y restar los bordes, consigo 8 + 6 - 12 = 2.
La fórmula de Euler establece que, siempre y cuando su poliedro es un poco de buen comportamiento, si se suman los vértices y las caras juntas, y restar los bordes, se consigue siempre 2. Esto será cierto si el poliedro tiene 4, 8, 12, 20 , o cualquier número de caras.
Importancia: Fundamental para el desarrollo de topología, que se extiende a cualquier geometría de superficie continua.
El uso moderno: Topología se utiliza para entender el comportamiento y la función del ADN, y es una parte fundamental del kit de herramienta matemática utilizada para comprender las redes como las redes sociales e Internet.
La distribución normal

¿Qué significa? Define la distribución normal estándar, una curva en forma de campana en la que la probabilidad de observar un punto es mayor cerca del promedio, y declina rápidamente a medida que uno se aleja.
Historia: El trabajo inicial fue por Blaise Pascal, pero la distribución entró en su cuenta con Bernoulli. La curva de la campana, ya que actualmente viene de matemático belga Adolphe Quetelet.
Importancia: La ecuación es la base de la estadística moderna. La ciencia y las ciencias sociales no existir en su forma actual sin ella. Diseño estadístico experimento se basa en las propiedades de la curva normal, y cómo estas propiedades se refieren a errores que pueden ocurrir cuando se toma una muestra aleatoria.
El uso moderno: Se utiliza para determinar si los fármacos son suficientemente eficaces en ensayos clínicos.
La ecuación de onda

¿Qué significa? Una ecuación diferencial que describe el comportamiento de las ondas, al igual que el comportamiento de una cuerda de violín vibra.
Historia: Los matemáticos Daniel Bournoulli y Jean D'Alembert fueron los primeros en describir esta relación en el siglo 18, aunque de forma ligeramente diferente.
Importancia: El comportamiento de las ondas se generaliza a las obras de manera sólida, cómo ocurren los terremotos, y el comportamiento del océano.
Las técnicas desarrolladas para resolver la ecuación de onda han sido muy útiles para resolver el mismo tipo de ecuaciones también.
El uso moderno: Las compañías petroleras estallar los explosivos, a continuación, leer los datos de las ondas sonoras resultantes de predecir las formaciones geológicas.
La transformada de Fourier

¿Qué significa? Describe los patrones en el tiempo como una función de la frecuencia.
Historia: Joseph Fourier descubrió la ecuación, que se extendía desde su famosa solución de una ecuación diferencial que describe cómo fluye el calor y la ecuación de onda anteriormente descrito.
Importancia: La ecuación permite patrones de ondas complejas, como la música, el habla, o imágenes, para su desguace, limpiado, y se analizaron. Esto es esencial en muchos tipos de análisis de señales.
El uso moderno: Se utiliza para comprimir la información para el formato de imagen JPEG y descubrir la estructura de las moléculas.
Las ecuaciones de Navier-Stokes

¿Qué significa? Las ecuaciones de Navier-Stokes son la ecuación de física fundamental que describe cómo funcionan los fluidos. El lado izquierdo es la aceleración de una pequeña cantidad de líquido, la derecha indica las fuerzas que actúan sobre ella.
Historia: Leonhard Euler hizo el primer intento de modelar el movimiento del fluido. Ingeniero francés Claude-Louis Navier y matemático irlandés George Stokes dieron el salto al modelo que todavía se utiliza hoy en día.
Importancia: Una vez que las computadoras se volvieron lo suficientemente potente como para resolver esta ecuación, aproximadamente, se abrió un campo complejo y muy útil de la física. Es particularmente útil en la fabricación de vehículos más aerodinámico.
Si bien podemos usar las computadoras modernas para hacer simulaciones prácticas aproximadas de la dinámica de fluidos que son útiles en la ingeniería, la búsqueda de una solución matemática exacta (o incluso saber si existe o no una solución exacta en todos los casos) es todavía una cuestión abierta, uno cuya respuesta es unido a un premio de un millón de dólares .
El uso moderno: Entre otras cosas, se admiten para el desarrollo de los modernos aviones de pasajeros.
Las ecuaciones de Maxwell

¿Qué significa? Traza la relación entre los campos eléctricos y magnéticos.
Historia: Michael Faraday realizó un trabajo pionero en la conexión entre la electricidad y el magnetismo, y James Clerk Maxwell lo tradujo a estas ecuaciones. Las ecuaciones de Maxwell para el electromagnetismo clásico eran lo que las leyes del movimiento de Newton eran para la mecánica clásica.
Importancia: ayudado a entender las ondas electromagnéticas, ayudando a crear la tecnología eléctrica y electrónica más moderna.
El uso moderno: radar, televisión y las comunicaciones modernas.
La segunda ley de la termodinámica

¿Qué significa? Energía y el calor se disipan con el tiempo.
Historia: Sadi Carnot primera postula que la naturaleza no tiene procesos reversibles. Matemático Ludwig Boltzmann extendió la ley, y William Thomson declaró formalmente.
Importancia: Es esencial para nuestra comprensión de la energía y el universo a través del concepto de entropía entropy.Thermodynamic es, en términos más o menos, una medida de la desordenada es un sistema. Un sistema que comienza en un estado ordenado, desigual - por ejemplo, una región caliente al lado de una región fría - siempre tenderá a igualar, con el calor que fluye desde la zona caliente a la zona fría hasta que esté bien distribuido.
El uso moderno: Termodinámica subyace en gran parte de nuestra comprensión de la química y es esencial en la construcción de cualquier tipo de planta de energía o en el motor.
La teoría de la relatividad de Einstein
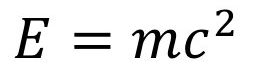
¿Qué significa? Energía y la materia son dos caras de la misma moneda.
Historia: La génesis de la ecuación de Einstein fue un experimento de Albert Michelson y Edward Morley demostró que la luz no se movió de una manera newtoniana en comparación con el cambio de marcos de referencia. Einstein hizo un seguimiento de este conocimiento con sus famosos trabajos sobre la relatividad especial (1905) y la relatividad general (1915).
La relatividad especial presentada en ideas como la velocidad de la luz es un límite de velocidad universal y el paso del tiempo es diferente para las personas que se mueven a diferentes velocidades.
La relatividad general describe la gravedad como una curvatura y plegado del espacio y el tiempo a sí mismos, y fue el primer cambio importante en nuestra comprensión de la gravedad ya la ley de Newton. La relatividad general es esencial para nuestra comprensión de los orígenes, la estructura, y el destino final del universo.
Importancia: Probablemente la más famosa ecuación de la historia. Cambió por completo nuestra visión de la materia y la realidad.
El uso moderno: ayudó a dirigir a las armas nucleares, y si el GPS no cuenta para él, sus direcciones estarían a miles de yardas.
La ecuación de Schrödinger

¿Qué significa? Esta es la ecuación principal en la física cuántica. Modelos de materia como una onda, en lugar de una partícula.
Historia: Louis-Victor de Broglie establecido claramente la naturaleza dual de la materia en 1924. La ecuación que se ve fue derivado por Erwin Schrödinger en 1927, la construcción fuera del trabajo de los físicos como Werner Heisenberg.En él se describe la forma en que las partículas subatómicas y los átomos evolucionan con el tiempo.
Importancia: revolucionado el punto de vista de la física a escalas pequeñas. La idea de que las partículas en ese nivel existe en una gama de estados probables fue revolucionario.
la mecánica cuántica y la relatividad general modernas son las dos teorías científicas más exitosas de la historia - todas las observaciones experimentales que hemos hecho hasta la fecha son totalmente coherentes con sus predicciones.
El uso moderno: La mecánica cuántica es necesario para la mayoría de la tecnología moderna - la energía nuclear, los ordenadores basados en semiconductores, láseres y están construidos en torno a los fenómenos cuánticos.
teoría de la información de Shannon

¿Qué significa? Calcula la cantidad de datos en un trozo de código por las probabilidades de sus símbolos de componentes.
Historia: Desarrollado por el ingeniero de los Laboratorios Bell Claude Shannon, en los años después de la 2ª Guerra Mundial.
Importancia: La ecuación dada aquí es para información de la entropía de Shannon . Al igual que con la entropía termodinámica dado anteriormente, esta es una medida del desorden. En este caso, se mide el contenido de información de un mensaje - un libro, una imagen JPEG enviado en el Internet, o cualquier cosa que se puede representar simbólicamente. La entropía de Shannon de un mensaje representa un límite inferior de la cantidad de mensajes que puede ser comprimido sin perder algo de su contenido.
El uso moderno: medida de la entropía de Shannon puso en marcha el estudio matemático de la información, y sus resultados son fundamentales para la forma en que nos comunicamos a través de redes de hoy.
El modelo logístico para el crecimiento de la población

¿Qué significa? Estimates el cambio en una población de criaturas a través de generaciones con recursos limitados. Es importante destacar que esta ecuación puede conducir a un comportamiento caótico.
Historia: Robert mayo fue el primero en señalar que este modelo de crecimiento de la población podría producir el caos en el año 1975. El trabajo importante por los matemáticos Vladimir Arnold y Stephen Smale ayudaron con la comprensión de que el caos es una consecuencia de las ecuaciones diferenciales.
Para ciertos valores de k, el mapa muestra un comportamiento caótico: si empezamos en algún valor inicial particular de x, el proceso va a evolucionar de una manera, pero si comenzamos a otro valor inicial, incluso uno muy, muy cerca del primer valor, el proceso evolucionará de una manera completamente diferente.
Importancia: Con l
a ayuda en el desarrollo de la teoría del caos, que ha cambiado completamente nuestra comprensión de la forma en que funcionan los sistemas naturales
Vemos un comportamiento caótico - el comportamiento sensible a las condiciones iniciales - como esto en muchas áreas. El tiempo es un ejemplo clásico - un pequeño cambio en las condiciones atmosféricas en un día puede conducir a sistemas totalmente diferentes de tiempo de unos días más tarde, más comúnmente capturado en la idea de una mariposa bate sus alas en un continente provocando un huracán en otro continente.
El uso moderno: Se utiliza para modelar los terremotos y pronosticar el tiempo.
El modelo Negro-Scholes

¿Qué significa? Precios un derivado basado en la suposición de que es libre de riesgo y que no hay oportunidad de arbitraje cuando se tasa correctamente.
Historia: Desarrollado por Fischer Negro y Myron Scholes, luego se expanden por Robert Merton. Los dos últimos ganaron el Premio Nobel de Economía 1997 para el descubrimiento.
Importancia: ayudó a crear el multi-billones de dólares derivados mercado ahora. Se argumenta que el uso inadecuado de la fórmula (y sus descendientes) contribuyó a la crisis financiera. En particular, la ecuación mantiene varios supuestos que no son verdad en los mercados financieros reales.
El uso moderno: Variantes todavía se utilizan para fijar el precio mayoría de los derivados, incluso después de la crisis financiera.


No hay comentarios:
Publicar un comentario